Continuous Time Signal

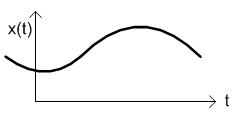
A continuous Time Signal is one whose value is defined at every instant of time i.e it gives continuous values unlike discrete time signal



A continuous signal or a continuous-time signal is a varying quantity (a signal) whose domain, which is often time, is a continuum (e.g., a connected interval of the reals). That is, the function's domain is an uncountable set. The function itself need not be continuous. To contrast, a discrete time signal has a countable domain, like the natural numbers.
The signal is defined over a domain, which may or may not be finite, and there is a functional mapping from the domain to the value of the signal. The continuity of the time variable, in connection with the law of density of real numbers, means that the signal value can be found at any arbitrary point in time.
A typical example of an infinite duration signal is:
f(t) = sin(t)